Сортировка Шелла

Описание

  При сортировке Шелла сначала сравниваются и сортируются между собой значения, отстоящие один от другого на некотором расстоянии d. После этого процедура повторяется для некоторых меньших значений d, а завершается сортировка Шелла упорядочиванием элементов при d=1 (то есть обычной сортировкой вставками). Эффективность сортировки Шелла в определённых случаях обеспечивается тем, что элементы «быстрее» встают на свои места (в простых методах сортировки, например, пузырьковой, каждая перестановка двух элементов уменьшает количество инверсий в списке максимум на 1, а при сортировке Шелла это число может быть больше).
  Невзирая на то, что сортировка Шелла во многих случаях медленнее, чем быстрая сортировка, она имеет ряд преимуществ:

• отсутствие потребности в памяти под стек;
• отсутствие деградации при неудачных наборах данных — быстрая сортировка легко деградирует до O(n²), что хуже, чем худшее гарантированное время для сортировки Шелла.

  При проведении экспериментов, для выбора длины промежутков используется предложенный Седжвиком метод:
    Перед сортировкой происходит вычисление длин промежутков, которые записываются в массив inc.
    Значение записываемого элемента вычисляется по формуле:
    
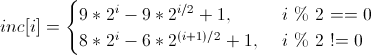
    Остановиться нужно на значении inc[i-1], если 3*inc[i] > размер массива.

Оценка сложности

Лучшая	Средняя	Худшая
n	n (log n)² или n^(3/2)	n (log n)²

Лучший случай

Массив уже отсортирован в правильном порядке. Количество сравнений в таком случае наименьшее

Худший случай

Если неправильно выбраны промежутки

Код